ハンバーガー統計学でMATLABに慣れる
10-4-2014 updated
MATLABに慣れるために,私が統計の基礎を学ぶのにとてもお世話になったハンバーガー統計学(1)を復習させて頂くことにしました。ストーリーに沿ってMATLAB を使いつつ,基本となるコマンドを解説します。リンク先を参照しながらご覧下さい。
1. 平均と分散
1-1. 変数の作成
ワクワクバーガーのポテトを買ったところ,49本入っていました。右の表がそれぞれのポテトの長さ(cm)です。本家では Excel を使っていますが,MATLAB でポテトの長さの平均値を計算してみます。
まず,MATLABを起動してポテトの長さを入れる変数を作ります。 New Variable をクリックすると,Excel のような入力画面が出てきます。MATLAB では,データは基本的に行列なので,この場合は 49行 x 1 列にポテトの長さを入れていくことになります。
手打ちで変数を入れていきましょう。または,Excel を経由すれば右の表からコピー & ペーストでいけるはずです。
別の方法として,Command window を使う方法があります。以下のコマンドをコピーして Enter を押してみて下さい。
| 3.5 | 4.9 | 2.8 | 4.2 | 4.4 |
| 3.8 | 5.2 | 5.6 | 5 | 4 |
| 5.8 | 6 | 5.7 | 4.7 | 5.5 |
| 6.4 | 3.9 | 5.1 | 4.1 | 4.2 |
| 4.2 | 5.3 | 4.4 | 3.7 | 4.8 |
| 4.2 | 4.6 | 5.6 | 4.9 | 3.7 |
| 4 | 3.9 | 5.3 | 4.7 | 3.1 |
| 3.6 | 4.2 | 3.9 | 5.3 | 4.7 |
| 3.8 | 4.2 | 5.1 | 3.6 | 5 |
| 5.2 | 6.4 | 3.6 | 4.2 |
>> unnamed=[3.5;4.9;2.8;4.2;4.4;3.8;5.2;5.6;5;4;5.8;6;5.7;4.7;5.5;6.4;...
3.9;5.1;4.1;4.2;4.2;5.3;4.4;3.7;4.8;4.2;4.6;5.6;4.9;3.7;4;3.9;5.3;4.7;3.1;3.6;...
4.2;3.9;5.3;4.7;3.8;4.2;5.1;3.6;5;5.2;6.4;3.6;4.2];
ここでは,コマンドウィンドウに打ち込む文字を青字で書くことにします。>> はもともと表示されている記号なので,実際には unnamed 以降を打ち込むことになります。
- コマンドウィンドウ: ここから様々なスクリプトや関数を実行する(2)。
- Current folder: 現在のフォルダに含まれているデータやスクリプトファイルの一覧。
- Workspace: コマンドウィンドウ上で実行された変数値などの結果がここに保存される。変数の名前等を知ることができる(2)。
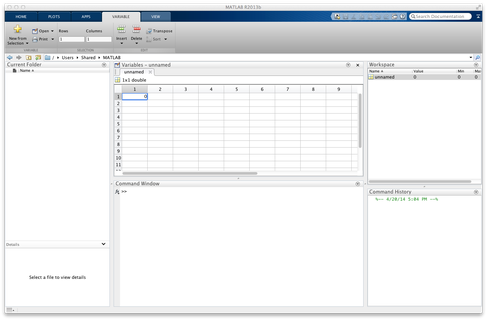
どちらの方法でも,ワークスペース Workspace に unnamed という変数が現れるはずです。 49 x 1 double という形式の行列です。この unnamed は W という名前に変えておきましょう。
>> W=unnamed;
最初の行は,W という新しい変数に unnamed を代入するという意味です。これを実行すると,Workspace に W が現れるはず。unnamed はもういらないので,
>> clear unnamed;
として消してしまいましょう。
>> who
とすると,
Your variables are:
W
と表示され,現在手元に wakuwaku という変数があることがわかります。who は R の ls() コマンドみたいなものです。
せっかくなので,このデータを W.mat として保存しておきましょう。
>> save W
現在のフォルダー current folder に W.mat が現れます。これで,いつでも W を呼びだして使えるようになりました。
1-2. 平均値などの計算
変数 W の平均は,
>> mean(W)
で計算できます。
ans =
4.5714
と表示されるはず。
ここでは,
>> A=mean(W);
>> A
A=
4.5714
という形で覚えておきます。理由は 2 つあって,
- 行末のセミコロン ; は,「コマンドウィンドウ上に結果を表示しない」 という意味です。平均値ぐらいなら良いですが,結果が長くなってくると使いたくなってきます。今のうちに覚えておきましょう。
- mean(W) の結果を A などと置いておかない場合,結果は ans という変数として保存されます。次に何かの計算を同じように行った場合,その結果も ans として保存され,mean(W) の値を上書きしてしまいます。そこで,なるべくこの ans を登場させない方法に慣れておくと,後々役立つはずです。
その他の作業も MATLAB ではコマンドを使って行うことできます。
>> B=std(W);
2. 信頼区間
今度は,ワクワクバーガーのポテトの本数が気になってきたようです。買ったポテトには49本入っていましたが,他のものには何本入っているのか?
他の人が買ったポテト10個を無作為に選び,本数を数えてみたところ,次のようになりました。
47
51
49
50
49
46
51
48
52
49
これを,ワクワクバーガーのポテトの本数ということで,wno という変数として MATLAB に保存します。同じく new variables というところから作るか,
>>wno=[47;51;49;50;49;46;51;48;52;49];
>> E=mean(wno);
>> F=var(wno);
で平均値 49.2 と不偏分散 3.51 をそれぞれ計算することができます。
次の問題として,この平均値 49.2 を母集団の平均値をみなしていいかどうかが問われています。無数にあるワクワクバーガーのポテトから,たった10個を選んで得た標本分散の平均値と分散は,母集団のものに一致するのか?
結論だけ示すと,標本集団の平均値は母集団のそれに一致し,また標本集団の不偏分散は母集団の分散に一致します。このあたりの詳細は分散 variance に詳しく述べてあります。区間推定の部分には,とくに MATLAB を使うような計算が出てこないので省略します。
3. カイ二乗検定
検定の詳細は chi square に示します。ここでは,ハンバーガー統計学の第3章「チキンの売り上げは少ないのか」をMATLAB を使って学習します。
ワクワクバーガーの売り上げは,ポテト435個に対してチキン165個で,チキンの販売個数は全体の約4割です。
一方,モグモグバーガーではチキン販売個数は全体の約5割ですが,この差が統計学的に有意と言えるのかどうか,というのが本章の問題です。
| お店 | ポテト | チキン | 合計 |
| ワクワク | 435 | 165 | 600 |
| モグモグ | 265 | 135 | 400 |
MATLAB には chi2 (chi square) を含む関数 function がたくさんあります(3)が,ここではカイ二乗適合度検定 chi2gof (chi-square goodnes-of-fit) を使います。
References
- ハンバーガー統計学 http://kogolab.chillout.jp/elearn/hamburger/index.html
- 小林 2014 (Book). 最新MATLABハンドブック 第5版. 秀和システム.
- http://www.mathworks.com/help/stats/chi-square-distribution-1.html