t 分布,t distribution
- 概要: t 分布とは
- t 分布の特徴
- 実際に t 分布を描いてみる
関連項目
t 検定を理解するために
この順で読んでみてください。
概要: t 分布とは
まず,2 つの集団を考えてみる。
- 母集団 parent population: 平均 μ,分散 σ2,標準偏差 σ の正規分布。
- この母集団からとってきた標本集団 sample population: 平均 m,不偏分散 u2,不偏分散の標準偏差 u。
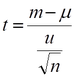
ここで,変数 t を以下のように定義する。分子は標本集団の平均から母集団の平均を引いたもの,分子は標本集団の標準偏差(不偏分散の標準偏差)をサンプル数 n の平方根で除したものである。
この t は統計検定量と呼ばれ, この t が従う分布を t 分布という。
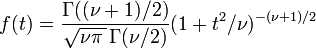
t 分布は左の式で表される。ここで,Γ はΓ関数,ν は自由度 degree of freedom(サンプル数 n から1 を引いたもの)である。
t 分布が考案された背景
実際の背景を反映していないかもしれないが,理解の順としては
- 仮説検定の手順として,検定統計量が必要である(仮説検定のページ)。
- 正規分布に従う z 値を用いた z 検定があるが,これを算出するには母集団の分散が必要。普通の実験では,母集団の分散は未知である(z 検定のページ)。
- そこで,標本集団のデータのみから算出できる t 値と,それが従う t 分布が考案された。
t 分布の特徴
-
t 分布は自由度のみの関数となり,母集団,標本集団の平均値や標準偏差に左右されない。
- n が大きいときは標本集団の「単なる標準偏差」を使うことができるが,n が小さくなるほど誤差が出てくるので,「不偏分散の標準偏差(n のかわりに n-1 を使う)」にしなければならない。
z 値とその他の t 値
t 値をネットで検索すると,そのサイトの説明の仕方に応じていろいろな式が出てきてしまい,これがまず混乱する。最初の段階として,t 値には,データの種類によって複数の計算式がある ことを認識しよう。
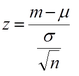
母集団と標本集団の平均,標準偏差が全てわかっている状態では,t 値に非常によく似た z 値が用いられる(左)。 これを用いる検定は z 検定である。
m は標本平均,μ は母平均,σ は母標準偏差(母集団の標準偏差),n は標本数。
論より証拠ということで,MATLAB を使って t がどのように分布するのか調べてみます。
- 母集団 parent population: 平均値 mean_p,標準偏差 sd_p
- 標本集団 sample population: 平均値 mean_s,標準偏差 sd_s,サンプル数 n
まずは,基本的な条件として mean_p=0, sd_p=1, 母集団の要素を 1,000,000 個,n = 100 としてみます。興味のある人は,右上のリンク先にある script も見てみて下さい。
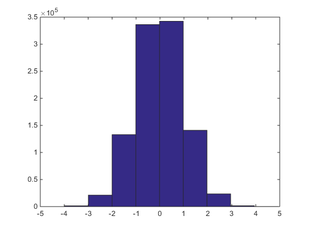
母集団のヒストグラム。縦軸は要素の個数です。
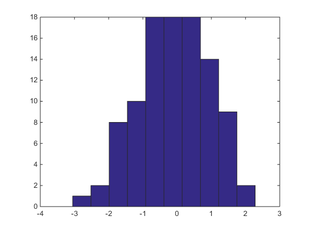
n = 100 の標本集団。母集団の分布をあまり反映していないように見えますが,ランダムサンプリングなのでこんなものです。
母集団から 100 個を取り出す作業を 1 回行い,上のようなヒストグラムを得ました。このときの t は -0.9636 でした。次に,「母集団から 100 個を取り出す」 作業を複数回繰り返し,t の値がどのように分布するのかを調べてみます。
10 回の繰り返し。まだ t の値はばらばらで,一定の傾向は見えません。
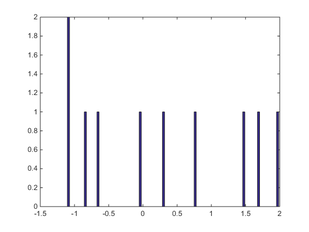
1,000 回。山型の分布になってきましたが,まだガタガタしています。

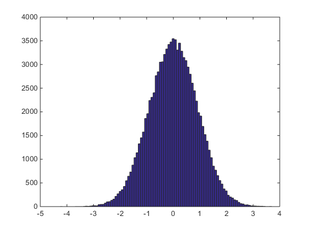
100,000 回。ほぼ理想的な分布になりました。
100 回。なんとなく,t は 0 に近い値を取る確率が高そうに思えてきました。
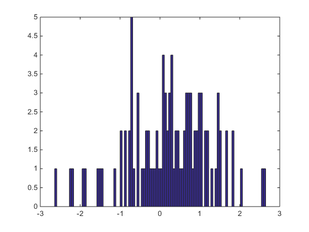
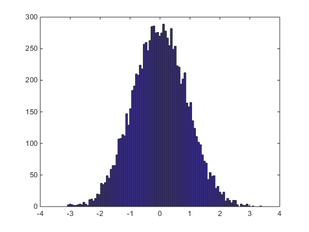
10,000 回。もう分布の形がはっきりわかるようになってきました。 ± 3 以上の値は極めて稀です。
References
- 検定統計量 T の式. Web.