一元配置分散分析 (One-way ANOVA) 

2018/11/10 Last update

 

このページは ANOVA @本家UBサイト に恒久的に移転しました。このページもネット上に残っていますが、最新の情報はリンク先を参照して下さい。

 


t 検定を理解するために

以下の順に読んで下さい。

  1. 仮説検定
  2. z 検定
  3. t 検定の原理 - 母平均の検定
  4. 対応のある t 検定
  5. t 検定メインページ
  6. Welch の t 検定: 分散が等しいと言えない場合
  7. Mann-Whitney の U 検定
  8. t 分布 t-distribution
  9. 実践: Excel での t 検定，平均値と分散を用いた t 検定

 

関連項目


概要: One-way ANOVA とは

このページでは，一元配置分散分析 one-way analysis of variance (ANOVA) について説明します。仮説検定 の考え方に馴染みのない方は，目次の 「t 検定を理解するために」 を先に読むことをお勧めします。

 

分散分析とは，試験の条件が結果に何らかの影響を与えたかどうかを，分散 variance を用いて調べる検定法 である（1）。 左側の図のようにデータが 2 群のときは t 検定を，右のように群が 3 つ以上のときは ANOVA を行い，結果が有意ならば多重検定を行うと覚えている人が多いだろう。


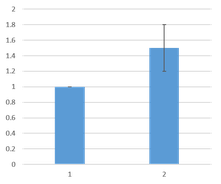
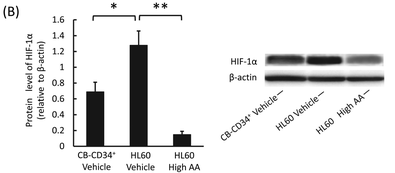
文献 2 より。


このページで解説する one-way ANOVA のポイントは以下の通りである。

 

  1. ある条件の影響の有無だけを検定する方法で，グループ間の比較は行わない。
  2. 条件が一つの場合は one-way ANOVA, 二つの場合は two-way ANOVA を使う。
  3. ANOVA なしで多重比較だけ行ってもよい場合がある。

 

検定方法の選び方の図も，参考に示しておく。


原理

まず，ANOVA は 正規分布している集団を対象としたパラメトリック検定 である（1）。　導入部分では，文献 1 の表現を参考にしている。


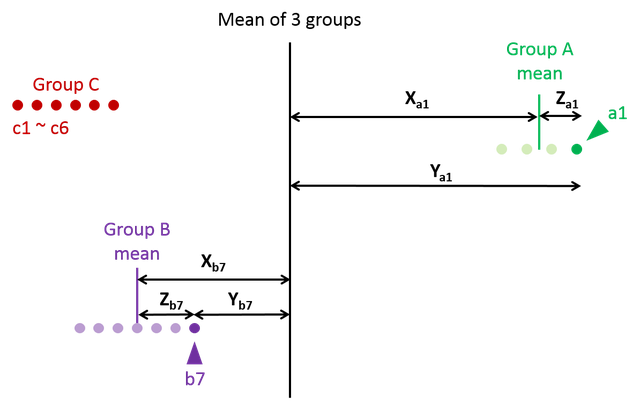
  1. サンプル数 N がそれぞれ 4, 7, 6 で平均値が異なる group A, B, C を上の図のように仮定する（1）。全サンプルの平均値が中央に来るように図を示してある。
  2. グループ A の要素 a1 について，図のように X, Y, Z を考える。図には a1 をつけて示している。
    • X = グループ A の平均と全体の平均の差
    • Y = 全体の平均と a1 の差
    • Z = グループ A の平均と a1 の差
  3. 同様に，グループ B の要素 b7 についても X, Y, Z を定義する。 b7 はグループ B の平均と全体平均の間にあるので，大小関係が異なることに注意する。
  4. このようにして，全ての要素について X, Y, Z を計算する。
  5. ここで発想を転換して，全ての要素を全体の平均値と X および Z で捉えなおす。つまり次のようなことである。

 

要素 a1 = 全体の平均値 + Xa1 + Za1

要素 a2 = 全体の平均値 + Xa2 + Za2

 

...中略...

 

要素 c6 = 全体の平均値 + Xc6 + Zc6

 

  1. いよいよ，X および Z の値と自由度 degree of freedom から，検定統計量 F を算出する。複数の段階があるので，以下のように分散分析表というものを作りながら算出することにする。この表は，統計ソフトでも分散分析の結果の一つとして表示されるはずである。
  2. この表では，X を要因，Z を誤差として扱う。理由は上の図を見れば理解できるだろう。 知りたいのは，Xa - Xc の違いに意味があるかどうかであり，このときに Z は邪魔な値（誤差）であるためである。
  3. 要因の自由度は 「グループの数 - 1」 であり，誤差の自由度は 「要素の数 - 1 - 要因の自由度」 になる。ここでは，要素が全部で 17 個なので，17 - 1 - 2 = 14 となる。
  自由度

偏差平方和 (sum of squares, SS)

（X または Z を全部 2 乗して合計）

平均平方 (mean square, MS) 分散比（F値）
X（要因） 2 Xa12 + Xa22 + ... + Xc62
 （X の SS）/（X の自由度）

（X の MS）/（Z

の MS）

Z（誤差）  14 Za12 + Za22 + ... + Zc62  （Z の SS）/（Z の自由度）  

 

  1. このようにして算出した F は，F 分布に従う変数になる。　F 分布は，2 つの自由度によって形が決まる分布である。したがって，ここでは 2, 14 という自由度において，得られる F の値がどれぐらい珍しいものであるかを このページの F 分布表などを参考に評価すればよいことになる。この辺りの考え方は，仮説検定のページでも説明している。
  2. 分子の X が全般に大きく，分母の Z が全般に小さいほど，F は大きな値をとることが予測できる。
  3. F がこのような値をとる確率が 5% 以下だったりする場合には，3 つのグループが同じ母集団に由来する（つまり有意差がない）と仮定するには F が大きすぎる（それぞれのグループの平均値 X が，誤差 Z を加味しても十分に離れている）ので，これらは違う母集団に由来する（つまり有意差がある）と考えることになる。
コメント: 0

References

  1. 池田 2013a. 統計検定を理解せずに使っている人のために III. 化学と生物 51, 483-495.
  2. Kawada et al. 2013a. High concentrations of L-ascorbic acid specifically inhibit the growth of human leukemic cells via downregulation of HIF-1a transcription. PLoS ONE 8, e62717.
  3. 東北大学動物遺伝育種学研究室 Animal breeding & genetics. Link.