カイ二乗検定（適合度の検定，独立性の検定）

11-28-2017 Last update

 

このページは カイ二乗検定 @本家UBサイト に恒久的に移転しました。このページもネット上に残っていますが、最新の情報はリンク先を参照して下さい。

 


  1. 概要: カイ二乗検定とは
  2. 適合度の検定
  3. 独立性の検定

 

関連項目

 

t 検定を理解するために

以下の順に読んで下さい。

  1. 仮説検定
  2. z 検定
  3. t 検定の原理 - 母平均の検定
  4. 対応のある t 検定
  5. t 検定メインページ: このページ
  6. Welch の t 検定: 分散が等しいと言えない場合
  7. Mann-Whitney の U 検定
  8. t 分布 t-distribution
  9. 実践: Excel での t 検定，平均値と分散を用いた t 検定

 

 


概要: カイ二乗検定とは

カイ二乗検定 chi square test とは，カイ二乗分布に従う統計検定量を用いる検定の総称である（1）。

 

  1. 標本集団の分布が，母集団の分布と一致しているかどうかを判定する適合度の検定
  2. 与えられた 2 つの集団の分布が一致しているかどうかを判定する独立性の判定

 

の 2 つがよく用いられる。

カイ二乗検定: 適合度の検定

適合度の検定 goodness-of-fit test は，標本集団の分布が母集団の分布と一致しているかどうかを判定する 検定である。

 

血液型の例（2）がわかりやすかったので，これを例示する。数字は元のページとは変えてある。

 

 

問題.

日本人の血液型の分布を A 型 40%，B 型 20%，AB 型 10%，O 型 30% とする。以下の血液型のデータは，日本人全体の分布と同じとみなしてよいか？

 

A 型 35 人，B 型 18 人，AB 型 6 人，O 型 41 人

 

カイ二乗検定

以下のように，期待度数（比率から期待される度数）と観測度数（実際のデータ）を比較する。

 

血液型 A B AB O 合計
期待度数 40  20 10 30 100 
観測度数 35 18 6 41 100

 

カイ二乗値は，以下の式で与えられる。

 

 

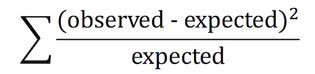
実際に数字をあてはめてみると，

 

(35 - 40)2/40 + (18 - 20)2/20 + (6 - 10)2/10 + (41 - 30)2/30 = 6.46

 

となる。この値がカイ二乗分布に従うことになる。なぜこの検定統計量がカイ二乗分布に従うのかは難しい問題なので，実際に検定を使いたいだけの場合は深く考えずに受け入れるのが良い。

 

コメント: 0

References

  1. 岩波 理化学辞典 第5版: 使っているのは 4 版ですが 5 版を紹介しています。
  2. カイ二乗分布. Link.