t 検定メインページ

2018/05/03 Last update

 

このページは  t検定の基礎 @本家UBサイト および  群間比較の目次・注意点 @本家UBサイト に恒久的に移転しました。このページもネット上に残っていますが、最新の情報はリンク先を参照して下さい。

 


このページの内容

  1. 概要: t 検定とは
  2. 対応のない t 検定の原理
  3. 実践的な注意点
    1. 検定方法の選び方（このページに詳細あり）
    2. 母集団が正規分布するということ
    3. 等分散性の検定（F 検定）後の t 検定
    4. t 検定の繰り返し
    5. 計数データの t 検定


t 検定を理解するために

以下の順に読んで下さい。

  1. 仮説検定
  2. z 検定
  3. t 検定の原理 - 母平均の検定
  4. 対応のある t 検定
  5. t 検定メインページ: このページ
  6. Welch の t 検定: 分散が等しいと言えない場合
  7. Mann-Whitney の U 検定
  8. t 分布 t-distribution
  9. 実践: Excel での t 検定，平均値と分散を用いた t 検定

 

関連項目


概要: t 検定とは

t 検定とは，t 分布 t-distribution に従う検定統計量 t を利用する検定法の総称である。一般に，2 組のグループ（標本）の平均値が有意に異なるかどうか という検定に用いられるが，以下のように様々なパターンがある。


  1. 2 群の母集団の平均値が等しいかどうか [帰無仮説: 等しい，対立仮説: 等しくない (有意差がある) ]
  2. ある集団（1 群）の母集団の平均値が特定の値に等しいかどうか [帰無仮説: 等しい，対立仮説: 等しくない] 
  3. 回帰直線を引いたときに，その勾配が 0 に等しいかどうか　[帰無仮説: 等しい，対立仮説: 等しくない]

 

このページでは，「対応がなく分散が等しいと仮定できる場合の t 検定の原理」 と，t 検定を使う際の実践的な注意事項を解説する。 t 検定について原理からよく理解したい人は，以下の順にページを読んでもらいたい。

 

  1. 仮説検定
  2. z 検定
  3. t 検定の原理 - 母平均の検定
  4. 対応のある t 検定
  5. t 検定メインページ: このページ
  6. Welch の t 検定: 分散が等しいと言えない場合
  7. Mann-Whitney の U 検定
  8. t 分布 t-distribution
  9. 実践: Excel での t 検定，平均値と分散を用いた t 検定

 

対応のない t 検定の原理

2 標本の分散が等しいと仮定できる場合

これまでと同様に，文献 8 の例題を使って進める。


例題

東地区と西地区からガソリンスタンドを 16 店舗ずつランダムに選び，価格を調査した。両地区の平均価格は同じと言えるか？ ただし，両地区の分散は同じと考えて良いものとする（文献 8 では，まず等分散性の検定をかけてから平均値の比較を行っている。この是非については下の 「等分散性の検定後の t 検定」 を参照のこと）。

東地区 119
 117 115 116 112 121 115 122 116 118 109 112 119 112 117 113
西地区 118
 115 115 122 118 121 120 122 120 113 120 123 121 121 109 117


分散が等しいと仮定できる場合は，対応のある t 検定とほとんど状況が変わらない（8）。 唯一異なるのは，標本数が等しいとは限らない ので，検定統計量を定義する際にこの点を考慮しなければならないことである。この問題は，併合分散 merged variance と呼ばれる分散値を使うことで解決する。


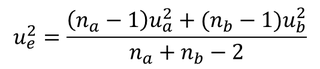
母分散の値はわからないが，2 標本の分散が等しいと仮定できるので，それらをプールした併合分散を考えることができる。

 

u2e は併合分散，u2a は 標本 A の分散，u2b は標本 B の分散，na は A の標本数，nb は B の標本数。


このとき，以下の検定統計量 t を定義することができ，これは自由度 na + nb - 2 の t 分布に従う。



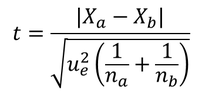
Xa, Xb は，それぞれの標本の平均値である。 あとはこの通りに t を算出し，通常の仮説検定を行えばよい。


ここのポイントは，等分散を仮定すると併合分散を導入できることである。


次は，分散が等しいと言えない場合の Welch の t 検定 へ進む。 


実践的な注意点

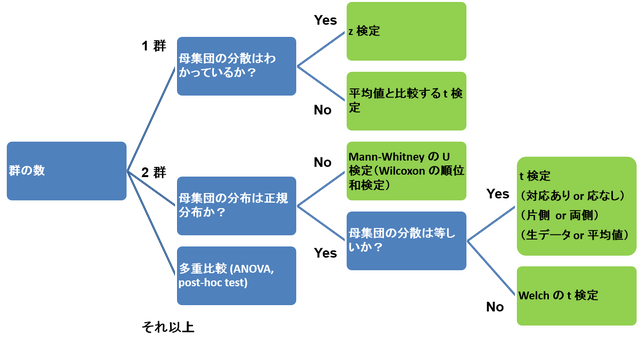
検定方法の選び方

以下のフローチャートに従って，適した検定を選ぶことができます。詳しくはそれぞれのページをご覧下さい。このページの下の方には，選択肢を選ぶに当たって参考になることなどが書いてあります。

母集団が正規分布するということ

t 検定の前提条件として，データが正規分布 normal distribution に従うことが必要である。これはしばしば誤解されるが，母集団が正規分布することを意味する。文献 1 から引用する。

 

「たとえば，平均値をt 検定で比べる場合には，動物を何匹か選んできて実験することになるんですけど，その背後にある動物の非常に大きな集団（母集団といいます）を考えたとき，何かの特性が正規分布しているかどうかが問題で，別に手元にきた100匹とか5 匹の動物（これをサンプルといいます）が正規分布しているかどうかは問題ではない んです．

 

正規分布から選ばれた代表なのかどうかが問題で，もし，背後にある集団で何かの特性が正規分布をしていれば t 検定というのは正確な方法となります．だから，t 検定は近似ではないんです．ただ，背景にある集団が正規分布していないと，必ずしも正確な方法にはなりません．」

 

> 母集団の分布を仮定しない方法をノンパラメトリック non-parametric な方法という（1）。

: 検出力（本当に差があるときに，差があると言える威力）が落ちる。


> 正規分布が仮定できなくても，左右対称の分布または対象数が多ければ，多くの場合は t 検定で問題ない（1）。

 

等分散性の検定（F 検定）後の t 検定

t 検定は母集団が正規分布することを前提としているので、何らかの方法で正規性を確認してから、t 検定またはノンパラメトリックな 

Mann-Whitney の U 検定 のどちらを使うか決めたくなる。


また，F 検定で分散が等しいかどうかを確認してから t 検定または Welch の t 検定 を使うことを推奨している例もある。


これらは、いわゆる事前検定 a priori comparisons の問題も含む複雑な問題である。主要な問題点は 2 つで，

 

  1. 有意水準 5% で、F 検定と t 検定を両方かけるので、全体の有意水準が 5% にならない。
  2. 仮に F 検定で等分散性が示唆されたとしても、これは仮説 hypothesis を考えると「等分散でない」 という仮説が棄却されただけで、「等分散である」 ことの根拠にはならない（6）。


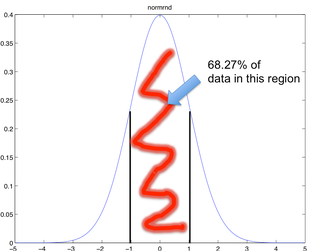
標準偏差、標準誤差 SD & SE のページにある標準正規分布。平均値 ± 1 SD にデータの 68.27% が含まれる。



1. の問題は，いわゆる多重検定の問題であるので，Bonferroni 補正などを利用して p 値を変更するという対処法もあるようだ（7）。


この項目は，F 検定を正規性の検定と間違えて書いていたので訂正しました（6-21-2015）。

計数データの t 検定


  • D さんと J さんが今まで食ったパンの枚数を比較する。
  • 組織切片で免疫染色を行い，染まった細胞の数を A 群と B 群で比較する。
  • A 群と B 群にストレスを与え，生き残った個体数を比較する。（普通は生存率で比較するが）

 

このようなデータは 計数データ であり，整数以外の値を取らない。したがって分布は正規分布にはならず，離散型の分布になる。このようなデータには，正規分布を仮定する t 検定を適用することはできず，ノンパラメトリックな Mann-Whitney の U 検定を使う必要がある。

 

しかし，リアルタイム PCR などで測定する mRNA 量も厳密には計数データである。これは，上で述べた 「数が十分に多く，分布が対称な場合には，だいたい t 検定で問題ない」　ということに基づいていると思われるが，この点も頭に入れておく必要があるだろう。

 

 

文献 8


t 検定の繰り返し

  • 第1種の過誤 type I error を t 検定を例に説明 

t 検定を繰り返すと第 1 種の過誤の確率が高まるので，避けなければならない。このような場合は分散分析 ANOVA を用いる。

 

これは，統計の教科書によく書かれている基本事項であるが，実際にどのような意味なのかを少し考察してみる。

 

右の図（2）では，何種類もある dlip という遺伝子について，一つずつを欠損させたショウジョウバエの変異体を作り，体重（mg）をオス（m）とメス（f）で測定している。

 

赤が変異体の体重，黒がコントロールの体重で，赤 vs 黒の t 検定を行っている。

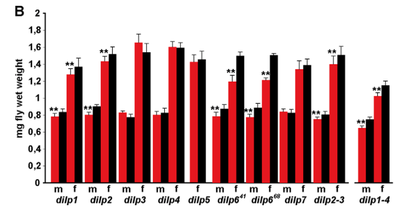
t 検定が何回も行われているが，これは「繰り返し」に当たらない。


 

合計 19 回の t 検定が一つの図で行われていることになるが，これは t 検定の繰り返しにあたるのだろうか？

また，概要の図でも同じように t 検定が 2 回繰り返されているが，これも問題だろうか？


実際にはこれは OK。ここではたまたま同じグラフに示しているので t 検定を繰り返しているように見えるが，これは 2 つのバーのグラフが 19 個並んでいるのと同じである。実際に問題となるのは下の図のような場合。


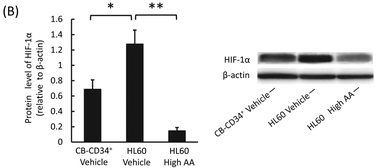
文献 4 の図。Western blot のバンドの太さを 3 群で比較しており，これが t 検定の繰り返しで，ANOVA を用いるべき事例である。



つまり，「t 検定を繰り返してはいけない」 というのは，同じデータに t 検定を複数回かけてはいけない ということである（3）。

標準化されたデータの t 検定

右のように，コントロール群の値が全て 1 でエラーバーがなく，実験群の値だけにエラーバーがついている図を見たことがあるだろうか。

 

これは，たとえば以下のようなデータ処理を経て出来上がっているグラフだと思われる。

  • マウスから細胞を初代培養する。
  • 薬剤 A をかけた実験群（右図の 2）と，A の溶媒のみをかけた対照群（右図の 1）について，何かを測定して棒グラフにする。
  • 初代培養の条件がうまく整わないので，実験ごとに値が大きく違ってしまうが，薬剤 A の効果は一定で，いつも測定値は 1.5 倍ぐらいになる。
  • そこで，それぞれの実験で常に対照群の値を 1 として標準化し，これを 5 回繰り返して右のグラフを作る（N = 5）。
  • 対照群のデータは，N = 5 だが全て値が 1 なので，エラーバーの長さは 0 になる。

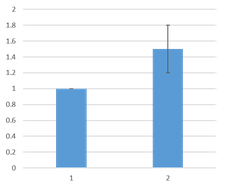
薬剤 A の効果について知りたい実験であり，初代培養の条件の影響を排除することは必ずしも悪いことではない。しかし，標準化したあとのデータに対して t 検定をかけることは，明らかに誤りである。なぜならば，t 検定の前提条件として母集団が正規分布に従うことがあるが，値が全て 1 である対照群からは，母集団の正規性を想定することができないためである。


ではどうすればいいのか，まだはっきりした答えがみつからないが，たぶんそれぞれの実験について 1 と 2 の値から算出される調整のための定数を定義して，それに対して両群の値を標準化すれば良いのではないかと思う。

この標準化が，t 検定の p 値に与える影響について，簡単なプログラムを組んで調べてみた。手順は以下の通り。

  • 集団 a は，平均値 1，標準偏差 0.5，要素 n 個で正規分布に従う。
  • 集団 b は，平均値 1.5，標準偏差 0.75，要素 n 個でこれも正規分布に従う。
  • n の値を 2 から 50 まで変化させたときに，a と b を t 検定かけたときの p 値がどのように変化するかを調べた。この結果が下の棒グラフ 1 で，一番左の坊が n = 2 ，一番右が n = 50 である。
  • 下の棒グラフ 2 は，要素 n 個で値が全て 1 の集団 c と，要素 n 個で値が全て b/a の集団 d についての同じグラフである。b の値を，a の値で標準化したあとに t 検定をかけているということになる。

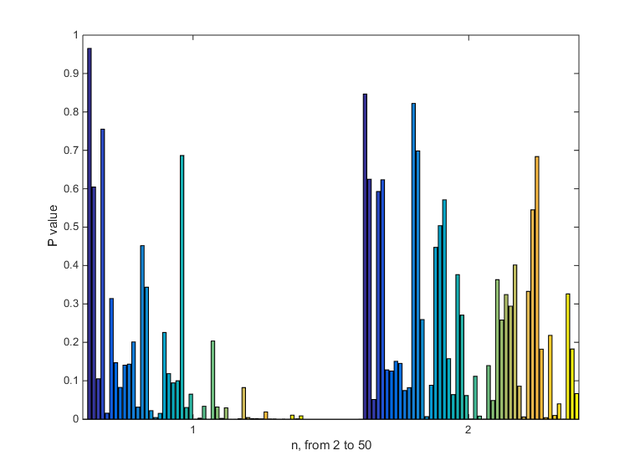
ここからわかることは，n の値が小さいときは，おそらく標準化によってバラツキか見かけ上少なくなるため（とくに a 群 → c 群の変換によって），p 値は標準化を行った 2 の方が小さい 傾向を示す。


しかし，正しい t 検定である 1 では，p 値が n に応じて順調に小さくなるのに対し，2 ではあまり小さくならないようである。c 群が不自然な分布（一様分布）をしていることが悪い影響を与えているのではないかと思う。


References

  1. 山中ら 2009a. 分子生物学，生化学，細胞生物学における統計のポイント. 蛋白質核酸酵素 53, 1792-1801.
  2. Gronke et al. 2010a. Molecular evolution and functional characterization of Drosophila insulin-like peptides. PLoS Genet 6, e1000857.
  3. t検定をばかにしてはいけない。の巻き。 Web.
  4. Kawada et al. 2013a. High concentrations of L-ascorbic acid specifically inhibit the growth of human leukemic cells via downregulation of HIF-1a transcription. PLoS ONE 8, e62717.
  5. Okumura's Blog; 2 段階 t 検定の是非. Web.
  6. 統計勉強: 等分散性の検定について. Web.
  7. Welch検定が主流，単純 t 検定や ANOVA は時代遅れ：Statwingの話題から. Link.
  8. 荒木 1988a. ジョジョの奇妙な冒険 第 3 巻. 講談社.