主成分分析: Principal component analysis
概要: PCA とは
主成分分析 (principal component analysis; PCA) とは,データに含まれる変数とは異なる指標を設定し,変数間の関係を把握しやすくするための統計手法である。身体検査の例(1)がわかりやすかったので,これを例に説明する。
身長と体重がデータとしてあるとき,おそらく両者は右図のように正の相関を示すだろう。
このデータに,「体の大きさ」という 新たな指標を導入すると,変数間の関係や特徴を把握しやすくなる。
要するに,このデータを「でかい人は身長も体重も大きい」と解釈できるようになるのである。
これが主成分分析の基本的な考え方で,この例では「体の大きさ」が 第一主成分 (PC1) と呼ばれる(1)。
もともと身長・体重という 2 種類の指標で表されていたデータを「体の大きさ」という指標で代表させるため,主成分分析によって 2 次元のデータを 1 次元のデータに変換したと考えることができる。ただし,これに伴って情報は損失している。
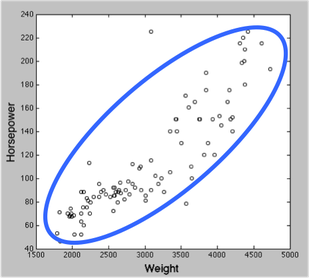
ピアソンの相関 のページにある自動車の重量と馬力の相関の図。横軸を体重,縦軸を身長だと考えてもらえると,このページでも参考になる。
元のページでは,「肥満の程度」というもう一つの新たな指標(第二主成分)を考えている。この場合はもとの変数が 2 つ,主成分分析によって生じた新たな指標が 1 or 2 個だが,多くの場合もとの変数はもっと多く,それを 2 つの新しい指標で代表させることが多い。
主成分は,各変数の線形結合として与えられる(1)。
寄与率
新たに作られた主成分(新しい指標)は,もとのデータをある程度表現しているはずである。この程度を表すものが 寄与率 である。
References
- 加納 2002a. 主成分分析 初心者向けテキスト. Pdf file.