生物学実験における統計 - 統計を使う上で意識すべきこと

2019/08/07 Last update

このページは生物学実験における統計 @本家UBサイトに恒久的に移転しました。このページもネット上に残っていますが、最新の情報はリンク先を参照して下さい。

t 検定を理解するために

以下の順に読んでみて下さい。

関連項目

母集団と標本集団

ラット 5 匹を使って実験を行った場合，通常はその結果が世の中の全てのラットで適用できるものと考える。これは，無意識に全てのラットを母集団，実際に使ったラットを標本集団と考えていることになる。

統計を適用する上では，この「母集団」と「標本集団」という概念が重要であるため，これを最初に意識するようにしよう。

「有意差」を問題とするような実験の多くは，標本集団のデータから母集団の性質を推定するという作業を目的にしている。

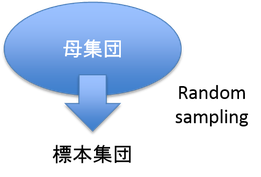
標本集団から，正しく母集団の性質を推定するためには，そのサンプリングがランダムであることが重要である。

統計は，基礎的見地から以下のように分類することができる（2）。上記の母集団と標本集団に関係する統計は，推測統計にあたる。

記述統計

得られたデータの特徴を客観的，効果的に記述するための方法で，ヒストグラム，相関図などの図による表現や，平均値，分散 standard deviation の算出などを含む。

推測統計

標本集団のデータから，確率論的に母集団の特性を推定するための方法をいう。仮説検定はこちらに相当する。また，内閣支持率，テレビの視聴率の算出なども推測統計である。

t-検定，ANOVA などの仮説検定（いわゆる「有意差が出る検定」）は，推測統計になる。つまり，得られたデータから母集団のデータを推測し，その結果に基づいて普遍的な議論を行うことが目的である。

これの意味するところは，統計は測定データ → 母集団という意味合いをもつもので，測定誤差 → 真の測定データという意味合いをもつものではないということである（3）。言い換えれば，n = 5 で実験をしたときに値が異なる理由は「個体差」であるべきで，「測定誤差」は含まれてはいけないということである。

このサイトで繰り返し述べていることだが，自分のデータをどのように示せばそのデータのもつ意味が伝わるかを考えることが最も大切であり，その上でデータを解釈するための道具として統計を考えるべきである。

有意水準を a とすると，実験を k 回繰り返したときの有意水準 a' は，

a' = 1-(1-a)^k

になる（4）。

有意水準が 0.05 のとき，「有意差がある」 = 「差が偶然ではない確率が 95% である」ということである。実験を何回も繰り返すと，この基準がだんだん甘くなっていくことは直感的にわかるだろう。

この問題は，同じ人（グループ）が実験を繰り返す場合に限らない。 100 のグループが，実際には差がない 2 つの群について，有意水準 0.05 で実験を行った場合を考えてみよう（4）。

理想的な場合には，95 のグループが「有意差がない」という結果を，5 のグループが「有意差がある」という結果を得るだろう。有意差を見出したグループのみが，その結果を論文にすると考えると，全く悪意がないのに，再現性のない論文があふれることになる。これを publication bias という。

コメント: 0

山中ほか 2009a (Review). 分子生物学，生化学，細胞生物学における統計のポイント. 蛋白質核酸酵素 54, 1792-1801. Available on web.
MathWorks 2009a. MATLAB における仮説検定の基礎.
池田 2013. 統計検定を理解せずに使っている人のために I. 化学と生物 51, 318-325. Web pdf.
山村 1998a. 土壌肥料学における数理統計手法の応用上の問題点. 日本土壌肥料学会誌，69, 649-653