エラーバーの意味と正しい使い方
2018/04/20 Last update
このページは 新・エラーバーの意味と使い方 @本家UBサイト に恒久的に移転しました。このページもネット上に残っていますが、最新の情報はリンク先を参照して下さい。
- 概要
- エラーバーの種類
- データ区間を示すエラーバー
- 信頼区間を示すエラーバー
- 標準偏差を示すエラーバー
- 標準誤差を示すエラーバー
- エラーバー 8 つのルール
t 検定を理解するために
以下の順に読んでみて下さい。
- 仮説検定
- z 検定
- t 検定の原理 - 母平均の検定
- 対応のある t 検定
- t 検定メインページ
- Welch の t 検定: 分散が等しいと言えない場合
- Mann-Whitney の U 検定
- t 分布 t-distribution
- 実践: Excel での t 検定,平均値と分散を用いた t 検定
関連項目
- 確率変数 Random variable
- 確率密度関数 Probability density function
- 標準偏差と標準誤差
- 信頼区間
〜 SD のエラーバーは母集団の分散を,SE のエラーバーは母集団の平均値が収まる範囲を示す 〜
このページは,実際に学位論文や原著論文を書く人に向けた実践用のページです。原理などの説明は関連項目を見て下さい。
概要: エラーバーとは
エラーバー error bar とは,右のような棒グラフに付いているバーのことで,一般に以下のものを示すことが多い(1)。
- データ区間 range
- 信頼区間 confidence intervals
- 標準誤差 standard error (SE)
- 標準偏差 standard deviation (SD)
折れ線グラフや散布図にもつくことがある。なんとなく,エラーバーが短いほうがバラツキの少ない良いデータのように見える。
しかし,異なるエラーバーは異なる情報を伝えるため,その意味を正確に理解するとともに,エラーバーが何を表しているかを図の説明にはっきりと書くことが重要である。
このページでは,それぞれのエラーバーの特徴についてまとめるとともに,文献 1 で提唱されているエラーバーに関する 8 つのルールなどを紹介する。

図1. ゼブラフィッシュを低酸素に曝したあとの生存率(%)を,予め軽い熱ストレスを加えた preconditioned (PC) 群と,熱ストレスなしの NO PC 群で比較したもの(文献2)。エラーバーは標準誤差を示している。
エラーバーの種類
データ区間を示すエラーバー Range error bar
右の図のように,実際のデータの分布を示すエラーバー。文献1では説明されているが,実際には見たことがない。
SD, SE のエラーバーの特徴をまとめると,以下の表のようになる。
標準偏差,標準誤差のページには,SD, SE の説明や n を増やすシミュレーションの図などが載っているので,そちらも参考にして下さい。
| 標準偏差 SD | 標準誤差 SE | |
| 見た目 | 長くてかっこ悪い |
短くて良いデータに見える |
| 意味 | 母集団および標本集団のバラツキを示す |
母集団の平均値が収まる範囲を示す |
| n が増えると | 母集団の SD に近づく | 0 に近づく |
| 使い方 |
母集団のバラツキにも興味があるとき |
平均値に興味があり,その精度を問題にしたいとき |
使い方については,文献 4 の説明が秀逸である。少し改変しつつ,同じ説明を使わせて頂く。
薬剤 1, 薬剤 2 を投与したとき,効果の平均値が同じ値であった,という結果が右のグラフである。しかし,データのバラツキ具合が両者で異なっていた。 1 の方が効果が均一で,良い薬剤であるという結論を導きたい。
このときは,SD のエラーバー が適当である。
データが正規分布 normal distribution に従うとき,平均値 ± SD の範囲にデータの約 3 分の 2(68.27%)が,平均値 ± 2SD の範囲にデータの約 95% が含まれる。したがって,平均値 ± SD のグラフを眺めることで,元のデータの分布を推察することができる のである。
もっとも,n がわかっていれば SE エラーバーから SD エラーバーを推測することができるので,SE のエラーバーからもデータの分布についての情報は得ることができる。

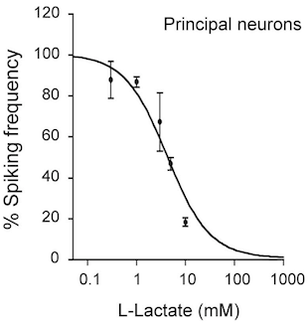
SE エラーバーは,右の図のようなデータで有効である。
右の図は,乳酸 lactate が神経 neuron の活動(発火 firing)を抑制することを示した実験の結果で,乳酸の IC50 を算出するために使われている。 しかし,ここで重要なのは図の内容ではなく,この SE エラーバーの意味である。
右の図でプロットされている値は,所詮は標本平均であり,真の値(母集団の平均値)を意味しない。しかし,一定の確率で SE エラーバーの範囲内に母平均があると考えてよい。したがって,右のグラフは帯状のグラフとして理解してほしい。
これが SE エラーバーの意味である。このように,平均値を使って何かの結論を導きたいときには,SE のエラーバー が適当である。
エラーバーの8つのルール
1. 図の説明に,エラーバーが何を意味するか必ず書く。
2. 図の説明に,n(サンプル数 or 独立した実験の数)を必ず書く。
3. エラーバーと統計は,独立した実験に対して適用される。
ルール 2 と 3 は,サンプル数 n と深く関連している。つまり,独立な試料または実験の数と,実験の繰り返し数 replicates とを区別するべきであるということである。
また,しばしば「何回か実験を繰り返して,代表的な例 representative results を示した」 というケースをみることがある。この図にエラーバーがついている場合,それは測定のエラーバーであると考えられる。したがって,本来はこのケースでエラーバーをつけるべきではない。全ての独立した実験の結果をプールし,各データから計算されたエラーバーをつけるのが正しい(1)。
4. 通常は対照群との比較に興味があるはずなので,SD ではなく,SE または信頼区間のエラーバーをつけるべきである。
ただし,サンプル数 n が少ない場合は,棒グラフにするよりもデータポイントをプロットする方がよい。
5. エラーバーの長さから,母集団の平均値の範囲を見積もることができる(意訳)。
「95% 信頼区間のエラーバーは,95%の確率で母集団の平均値 µ を含むことになる。n > 10 のとき,標準誤差 SE のエラーバーを約 2 倍すると 95% 信頼区間と同程度の長さになる。n = 3 のときは,約 10 倍しなければならない。」のような内容が,ルール 5 として書かれている(1)。
6, 7. エラーバーの長さから,有意差があるかどうか推察することができる(意訳)。
ルール 6, 7 として,以下の 2 つの例が載っている。
ルール6
n = 3 の 2 つのデータ群で,SE エラーバーがちょうど重ならないぐらいのとき,P 値は 0.05 に近い値である。n > 10 のとき,SE と同じぐらいの差が P = 0.05, SE の 2 倍の差が P = 0.01 程度と考えてよい(1)。
ルール7
n = 3, 95% 信頼区間のエラーバーがあるとき,エラーバーがほぼ重なっている場合に P = 0.05 程度である。半分重なっていると P = 0.01 程度である(1)。
8. 同じグループの繰り返し測定では,ルール 5 - 7は適用できない(意訳)。
繰り返し測定の場合,それぞれの値が独立でないために,有意差があるかどうか見積もるためにエラーバーを使うことができない。