確率密度関数 Probability density function
確率 probability,確率変数 random variable は,リンク先にそれぞれ説明があります。
ここは確率密度関数 probability density distribution のページですが,しっかりと理解するために確率分布 probability distribution と合わせて説明します。
- 離散型の確率変数
- 確率分布
- 確率密度関数
- 離散型分布の例
- 連続型の確率変数
- 確率分布
- 確率密度関数
- 連続型分布の例
- 累積分布関数
関連項目
- 確率 Probability
- 確率変数 Random variable
分布など
- 正規分布 Normal distribution
- t 検定 t-test, t 分布 t-distribution
離散型の確率変数
離散型の確率分布
確率分布 probability distribution は,辞書,教科書で以下のように定義されている。
- 確率変数 X のとる値 x が実軸上の領域 A に含まれる確率を A の関数として表したもの。確率空間(Ω, B, P)の測度,すなわち確率 P によって P(X ∈ A) のように与えられる(6)。
- 一般に可算集合 {x1, x2, ...} の中の値をとる確率変数 X は離散型といわれ,それぞれの値の確率 P(X=xk) = f(xk) を確率分布という(5)。
つまり,確率について次元のようなものを考えるならば,確率分布の次元は確率自身である。実例として,正 5 面体の理想的なサイコロでを考えてみる。

確率変数は 1, 2, 3, 4, および 5 であり,それぞれの値がもっている確率は 0.2 である。
確率分布とは,0.2 という値が散らばっているパターンそのもの のことをいう。
パターンなので,視覚化するならば右の plot の図全体に相当する。
この例では,サイコロは 1 - 5 以外の値をとらないため,離散型の確率分布 discrete probability distribution と呼ばれる。
Bar graph は値に範囲がある連続型の確率分布のように見えてしまうので,この場合よい表現方法ではない。
MATLAB で描画。
文献 2 では,次のように定義されている。上記の点を違う言葉で述べていると考えてよい。
- 確率空間が k 個の要素(これを単純事象という)1, 2, 3, ..., k から成り立つとする。
- 確率変数 X の取りうる全ての値 x1, x2, xk に対して,その値をとる事象 E1, E2,..., Ek と,それぞれの確率 p1, p2,..., pk が決まる。確率変数は大文字で書くのが決まりらしい(4)。
- このとき,事象 i にその確率 pi を対応させる対応を離散確率分布という。
離散型の確率密度関数
x について積分することによって,確率分布を与えるような関数 f(x) を確率度密度関数 probability density function という。辞書での定義は以下の通りである(6)。f が確率密度を示し,その関数を確率密度関数と呼ぶと書かれている。
なお,以上の確率分布,確率密度関数の定義は,離散型および連続型のいずれにもあてはまるものである。
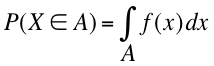
離散型の場合は,少し関数をイメージすることが難しい。
P(X=1) = P(X=2) = P(X=3) = P(X=4) = P(X=5) = 0.2
というのが確率密度関数 f(x) になる。
離散型分布の例
| データ範囲 | 分布の名前 | 説明 |
| 有限 |
ベルヌーイ分布 |
確率 p で事象 A が,確率 q = 1 - p で 事象 B が起こる分布である。両者の確率から,起こり得る事象は A および B の 2 つだけであることもわかる。コイントスが代表的な例。 |
| 有限 |
一様離散分布 |
上のサイコロの例のように,有限な数の事象があり,かつそれぞれの確率が等しい分布。「同様に確からしい」という表現がよく使われる。 |
| 無限 |
ポアソン分布 Poisson distribution |
1 時間当たりに受け取るメールの数,年間の交通事故数のように,自然数を要素とする確率変数 X が従う分布。 |
連続型の確率変数
確率分布
身長や体重は,サイコロの目のように離散的な値をとらず,連続的な分布を示す。単純化のために,正規分布 normal distribution に従うと考える。
この場合は,上記の例のように 0.2 などの数値の羅列で分布のパターンを記述することはできず,連続的な関数で記述する必要がある。
連続型の確率変数の場合も,分布のパターン(グラフそのもの)を確率分布といい,確率の分布を記述している関数(下のグラフの青線を示す式)を確率密度関数という。
確率密度関数
ここで,連続的ということは,以下のことを意味する。
- 身長はサイコロの目のように,有限な数の要素にわけることができない。
- つまり,右のグラフの線はいくら拡大しても線であり,点の集合ではない。
- 逆に言えば,たとえば身長が正確に 165 cm である確率はゼロである。
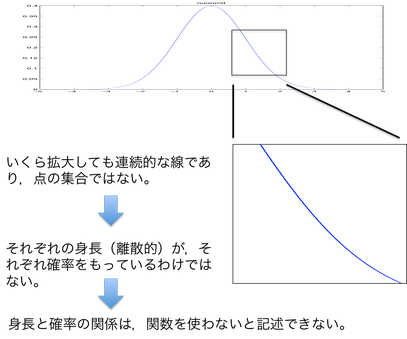
図 1.
確率密度関数は,もともと積分することで確率を与える関数として定義されている。
つまり,身長が 165 cm である確率はゼロであるが,165 - 170 cm のように範囲を指定すると,その範囲の積分値(右のグラフの赤い領域)が確率を与えることになる。
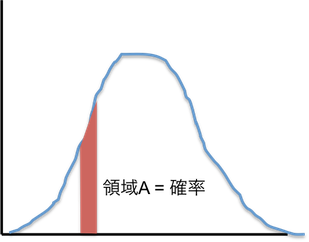
図 2.
連続型分布の例
文献 3, 5 などを参考にしました。
| データ範囲 | 分布の名前 | 説明 |
| 有限 |
ベータ分布 |
分布形状の自由度が高く,様々な分布にフィットさせることができる。 |
| 有限 |
ジョンソン SB |
ベータ分布と同様に自由度が高い。平均,標準偏差,歪度,尖度を自由に調整できる。樹木の幹の直径の分布? |
| データ範囲 | 分布の名前 | 説明 |
| 半無限 | 指数分布 | たまに起きる事象の「間隔」の分布。この分布に従って事故が発生すると,その頻度はポアソン分布になる。 |
| 半無限 |
対数正規分布 |
正規分布 normal distribution の対数。年収などがこの分布に従うらしい。 |
|
半無限 |
カイ二乗分布 |
カイ二乗検定 chi-square test に利用される。 |
|
半無限 |
F 分布 |
F 検定に利用される。 |
| データ範囲 | 分布の名前 | 説明 |
| 無限 | コーシー分布 | 正規分布に似るが,外れ値の多い分布である。 |
| 無限 |
ロジスティック分布 |
正規分布に似るが,裾が少し厚い。正規分布よりも式が簡単で扱いやすい。また,この分布の累積分布関数はロジスティック曲線であり,様々な分野で応用されている。 |
| 無限 |
正規分布 |
平均値と分散 SD で決まる基本的な分布。 |
| 無限 | t 検定 に利用される。 |
累積分布関数 Cumulative distribution function
まず,確率変数 X が A 以下の値をとる事象を {X ≤ A} とする。決まった範囲でなく 「A 以下の全ての値」
-∞ ≤ X ≤ A であることに注意しよう。
このとき,この確率は P(X≤A) = F(x) という関数で表される。関数 F(x) を 累積分布関数 cumulative distribution function, CDF という。
横軸に x ,縦軸に F(x) をとり,累積分布関数の図を描いてみよう。以下のことから,大体の形をイメージできるだろう。
- F(x) はあくまで確率なので,正の値をとり,かつ 1 を超えない。
- x が ∞ のとき,F(x) は 「確率変数 Y が無限大以下である確率」 である。つまり F(x) = 1 である。
- 逆に,x が - 無限大に近づくと,F(x) は 0 に近づいてゆくだろう。
したがって,F(x) は右のように F(x)=1 と F(x)=0 を漸近線するグラフになる。
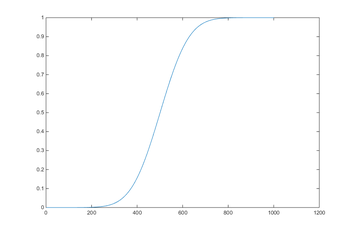
図 3.
X 軸の数値は適当なので,グラフの形をイメージするために使って下さい。
よく言われるのが,「累積分布関数を微分すると確率密度関数になる」 ということである。これは全く正しいが,積分から考えたほうがイメージしやすいのではないかと思う。
- 積分とは,関数と軸の間の面積を計算することである。
- 累積分布関数を微分すると確率密度関数になるのだから,逆に確率密度関数を積分すると累積分布関数になる。
これらのことを踏まえた上で,図 1 または図 2 で関数と X 軸の間の面積を左の方から(-∞ から)足し合わせていくイメージで考えてみよう。
-
x は -∞ まで及んでいるが,x が小さいときは確率もとても小さいので,x
を増やして行っても面積の増加はわずかである。
- x が 0 に近づくと,次第に増加率も大きくなっていく。
- この図は x = 0 に対して左右対称であり,かつ x = ∞ までの面積を全部足すと 1 になる。したがって,x = 0 のとき,ちょうど面積は 0.5 になり,そこから増加率が徐々に減ってゆく。
- x が正の ∞ に近づくと,増加率は非常に小さくなる。
x を動かしていったとき,その面積の変化がそのまま累積分布関数 F(x) になる ことがイメージ出来ただろうか?
References
- 岩波理化学辞典 第 4 版. 1995.