標準偏差と標準誤差, SD and SE
- 標準偏差, SD
- 不偏標準偏差 SD
- 標本標準偏差
- 変動係数 CV
- 標準誤差, SE
- サンプル数 n を増やすことの意味
t 検定を理解するために
以下の順に読んでみて下さい。
- 仮説検定
- z 検定
- t 検定の原理 - 母平均の検定
- 対応のある t 検定
- t 検定メインページ
- Welch の t 検定: 分散が等しいと言えない場合
- Mann-Whitney の U 検定
- t 分布 t-distribution
- 実践: Excel での t 検定,平均値と分散を用いた t 検定
関連項目
-
統計の目次
- 生物学実験における統計 - 最初に意識すべきこと
- 実験手法の目次
- 情報科学の目次(ソフトの使い方など)
- 確率変数 Random variable
- 確率密度関数 Probability density function
- 信頼区間
- エラーバーの意味と使い方
〜〜 SD は母集団のバラツキを表し,SE は母集団の平均とのずれを表す 〜〜
標準偏差, standard deviation, SD
不偏標準偏差
不偏標準偏差 standard deviation (SD or σ) とは,不偏分散 unbiased variance(しばしば シグマの2乗 σ2 で表される)の平方根であり,以下の式で表される(1)。ただし,X は全てのデータの平均値,xi はそれぞれのデータの数字,n は全てのデータの数である。
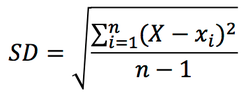
意味合いとしては,
- 平均値から個々のデータの値を引く。
- これを全部足し合わせたいのだが,値がプラスの場合とマイナスの場合があるので,それぞれを二乗してから足し合わせる。
- それを自由度(データの個数 - 1)で割る。
なので,個々のデータの値が平均値から離れているほど,不偏標準偏差は大きくなる ことがわかるだろう。つまり,不偏標準偏差とは データのバラツキの度合いを示す指標 であり,正規分布 normal distribution であれば,平均値 ± SD の範囲にデータの約 3 分の 2(68.27%)が,平均値 ± 2SD の範囲にデータの約 95% が含まれることになる。
このバラツキは標本集団のバラツキではなく,母集団のバラツキである(5)。 「サンプル数 n を増やすと,SD と SE の違いがはっきりと見えてくる」 の項を参照のこと。
右の図は,標準正規分布における平均値と SD の関係を示したもの。
このページに従い,MATLAB の normrnd 関数で平均 =0, SD = 1 の正規分布に従う乱数を 10,000 作ってプロットした。
この SD の特徴から,逆に異常値について考えることもできる(1)。つまり,平均値 ± 2SD の間に 95% の値が含まれるわけだから,たとえばあるデータの値が平均値 ± 2SD 以上であったら,その値は少なくとも全体の5% という珍しい値であることになる。

ただし,不偏標準偏差がデータのバラツキを示す指標として適切なのは,データの分布が正規分布に近いときのみである(3)。たとえば
- 高い値と低い値が多いような谷型の分布
- 外れ値が多いような分布
では不偏標準偏差は非常に大きくなる。このような場合は,平均 mean も集団を表す値として適切ではなく,中央値
median などを用いるべきである。
標本標準偏差
変動係数 Coefficient of variation, CV
SD の計算式から,平均値(または各データの値)が大きいほど不偏標準偏差も大きくなることがわかる。
データをグラフにしたときのエラーバーは通常 SD または SE なので,値が大きいほどエラーバーも長いことになる(右図, 文献2より)。データを扱ったことのある人ならば,これは感覚的に理解できるだろう。
したがって,平均値の異なるデータ群のばらつきの大きさを比較したい場合には, SD(またはSE)の比較は不適切である。

そこで,ばらつきの指標となる変動係数 coefficient of variance, CV が次の式で定義される。
CV = 不偏標準偏差/平均値
標準誤差, standard error, SE
標準誤差 standard error は,不偏標準偏差をサンプル数の平方根で割ったものであり,
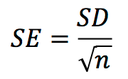
で与えられる。この値の意味するところは,以下のように説明できる。
-
母集団からある数の標本を選び,その平均値を計算する。この平均値を 標本平均 と呼ぶ。
-
この操作を何回も繰り返すと,当然標本平均にもバラツキが生じる。
-
標本平均の標準偏差を標準誤差 standard error of means (SEM) という。
標準誤差はさまざまな統計量に対して定義できるが,単に標準誤差と言った場合はこの「標本平均の標準誤差」のことを指す。このことをちゃんと表現したい場合は,英語ならば SE ではなく SEM を用いる方が良い。
標本平均の不偏標準偏差から,上の式を導く仮定はややこしいので,いずれ別のページでまとめることにする。文献 4 にその過程が示されている。
サンプル数 n を増やすと,SD と SE の違いがはっきりと見えてくる
n を増やしたときの SD の変化
生物学実験では,原則として母集団の平均値,分散,不偏標準偏差はわからないので,標本についてデータを得て,そこから母集団の値を推測するという手順を踏んでいる。
サンプル数 n を増やしていくと,それは母集団の標本数に次第に近づいてゆく。このとき,標本集団の平均値 m は,次第に母集団の平均値(真の平均値)M に近づいていくだろう。分散は,母集団の分散に近づいていく。分散の平方根である不偏標準偏差も,母集団の標準偏差に近づいていく。
n を増やしたときの SE の変化
一方,標準誤差 SE は何に近づいていくだろうか? これは 0 に近づいていくのだが,以下のように複数の説明が可能である。実際には,どれも同じことを言っている。
- SE は SD をサンプル数 n の平方根で割ったものなので,n が大きくなると 0 に近づいてゆく。すなわち,母集団が非常に大きいと仮定すると,分母は限りなく大きくなるが,分子は母集団の標準偏差付近で足踏みしていることになる。母集団の正規分布を仮定する限り,不偏標準偏差は有限のそれなりの値である。
- 母集団から標本をとってその平均値(標本平均)を計算するとき,標本数 n が大きくなると,標本平均は 「母集団と同じ平均値をもち,標準偏差 SE の正規分布」に近づく。これを中心極限定理 central limit theorem という。n が大きくなると,標本平均は母集団の平均の近くに集まる。
- 標準誤差は,母集団の平均が収まる範囲を推定するものであり(1),母集団,n がともに極めて大きい場合,両者の平均値はほぼ一致して,標準誤差はほぼ 0 になる。
寿命 lifespan の平均が 85 歳,標準偏差が 10,50,000,000 人から成る母集団を考える。ここから n 人から成る標本集団を選んで,寿命の平均値,SD, SE を算出する。 n を 2 から 1000 まで変化させたとき,これらの値はどのように変化するだろうか?
結果は下の図の通り。
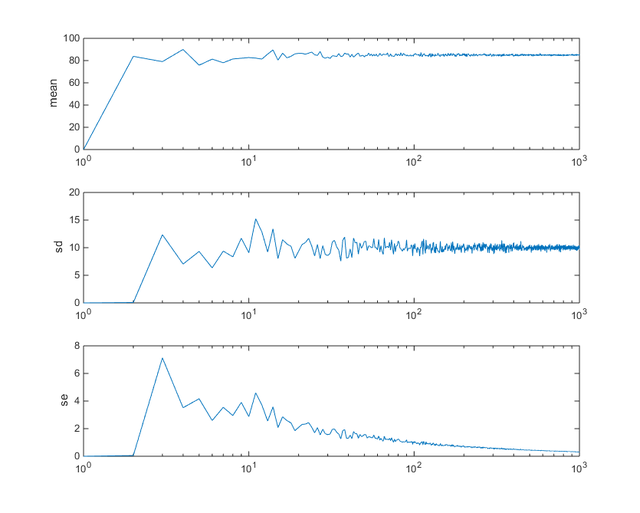
上から平均値,SD,SE の変化である。横軸は n の対数で,2 から 1000 までを検討した。標本集団の SD は,n が大きくなると母集団の SD である 10 に収束する。ただし,n が小さいうちは 10 ± 5 程度の範囲に散らばる。したがって,
- 標本集団の SD は母集団のバラツキ(標準偏差)の推定値 である。
-
しかし,標本集団のデータの質が低い場合(実験的要因によってばらついている場合,n
が不十分な場合など)には,当然そこから推定される母集団のバラツキも大きくなる。
- 結果として,SD が標本集団のバラツキのように見えてしまうこともある。または,SD は母集団のバラツキと,n が少ないことなどによる評価のバラツキの和になるとも言って良いか。
一方,SE は単調に減少し,n = 1000 でもまだ減少傾向を保っていることがわかる。平均値も 85 に収束しており,n が増えるほど精度の高い推定ができていると考えられる。
管理人 (月曜日, 27 7月 2015 18:07)
コメントありがとうございます。「サンプル数」は実験に使った個体数をイメージしていました。
たとえば一匹のマウスで体重を複数回測定する場合などは,マウスの数(サンプル数)<データ数ですが,
そうでない場合はサンプル数=データ数になると思います。
上の例のような「母集団からのランダムサンプリング」が頭にあるときは,サンプル数という言葉を使っていますが,
「データ数」という言葉の方が正しい気がしてきました。紛らわしくてすみません。そのうちもう少し調べてみます。
めい (月曜日, 27 7月 2015 02:44)
わかりやすい解説をありがとうございます。
とても基本的なことに対する質問で申し訳ないのですが、
データ数nとサンプル数nの違いは何なのでしょうか?
サンプル数はサンプルをとった回数ととらえてよろしいでしょうか。
よろしくお願いします。