分散 Variance

2020/03/20 Last update

 

このページは 分散 @本家UBサイト に恒久的に移転しました。このページもネット上に残っていますが、最新の情報はリンク先を参照して下さい。

 


  1. 定義: いろいろな分散
  2. 分散の意味と注意点
  3. Excel による分散の計算

定義: いろいろな分散

分散 variance にはいくつか種類がある。

 

  • 母分散 population variance
  • 標本分散 sample variance
  • 不偏分散 unbiased variance (or unbiased estimate of variance, unbiased estimate of population variance)

 


母分散 Population variance


m 個のデータ（x1, x2, x3, ... xm-1, xm）から成る母集団があり，X をその平均としたとき，母分散 σ2 は

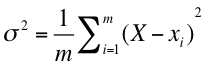
と表される。なお，X - xi を偏差 deviation という。

 

ただし，通常の生物学実験では，母集団についてのデータを得ることはできない。たとえば，マウスを使ってある実験を行ったとき，世界の全てのマウス（母集団）について実験を行うことはまず不可能である。しかし，実験から得られた知見（「薬剤Aを投与するとBという反応が起こる」など）は全てのマウスに当てはまることが期待される。

 

したがって，実験に使っているのは標本集団であり，得られたデータの分散は次に示す標本分散 sample variation である。そして，いかに標本分散から母分散を推定するかということを考える必要が出てくる。



 

標本分散 Sample variation


n 個のデータ（x1, x2, x3, ... xn-1, xn）から成る標本集団があり，X をその平均としたとき，標本分散 s2 は

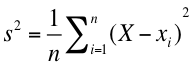
である。 Sample variation なので，s2 で表されることが多い。


つまり，全ての要素について平均値からのずれ（偏差）を2乗し，その平均をとったもので，式の形は母分散と同じである。母集団についてデータを得ることができないので，この標本分散から母集団を推定することになる。

 

ただし，一般に使われるのは以下に示す不偏分散であり，標準偏差 standard deviation も不偏分散から求めるのが普通である。



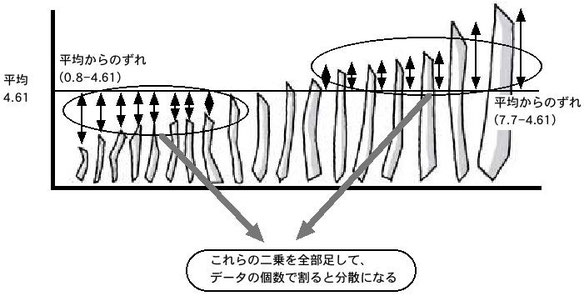
ハンバーガー統計学 1.3 より引用

  • (X - xi) を 2 乗しているのは，値を正にするためである。こうしないと，平均値よりも大きいばらつきと，平均値よりも小さいばらつきが相殺して，総和は 0 になってしまう。
    • この目的だと 4 乗でも 6 乗でも絶対値をとっても良いのだが，他の公式と関連づけるためには2 乗が最も都合がよい（2）。
  • n で割っているのは，サンプル数の影響をなくすため。こうしないと，サンプル数が多いほど総和が大きくなってしまい，サンプル数が異なる集団のばらつきを比較することができない。

 

不偏分散 Unbiased variance


上記の標本分散 sample variance は，母分散 population variance の推定値にはならないことが統計学的に証明されている。そこで，母分散と同じ期待値をもつ以下の不偏分散 unbiased variance が使われる。形の上では，単に n を n - 1 にしただけである。　-> なぜ n が n - 1 になるのか？

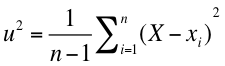
Unbiased variation なので，u2 と表されることが多い 。 しかし，u を表す決まった言葉はないようで，

 

  • 母標準偏差の不偏推定値
  • 不偏分散から求めた標準偏差
  • 標本に基づいて予測した標準偏差


などのような多様な表記がある（3）。単に標準偏差と書いてある場合は，n ではなく n-1 を使ったこちらの分散の平方根を意味する。 Excel の関数 =stdev も不偏分散であり，分母に n をおきたい場合は =stdevp を用いる（Excel Mac 2011 で確認）。

 

分散の意味と注意点


分散 σ2 はバラツキを表す指標であるが，2 乗しているために平均値と次元が異なる。そこで，分散の平方根である標準偏差 σ standard deviation もよく使われる。


ただし，これはその分布が正規分布に近いときのみであり，そうでない場合にはバラツキの指標としては不適切である。同様に，そのような場合には平均値も集団を代表する値とは言えなくなる。

 

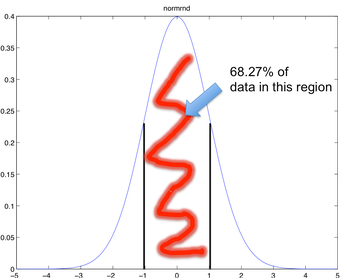
左の図は標準偏差のページで使っている平均 0，分散 = 標準偏差 = 1の正規分布（標準正規分布）である。

 

分散および標準偏差が大きいと，潰れたような形のべたっとした分布になる。しかし，たとえば左下の図のような2つのピークがある分布では，分散や標準偏差という概念があまり意味がないことがわかる。

 

また，分散では偏差を2乗するので，平均との差が大きく評価される。そのため，左下のような分布では分散は図からイメージされるよりもかなり大きくなる。



Excel による分散の計算

Excel の関数 =stdev は，分母に n ではなく n - 1 を置いた不偏分散である。n を使う場合は =stdevp を用いる。（Excel Mac 2011 で確認）

コメント: 0

References

  1. ハンバーガー統計学 http://kogolab.chillout.jp/elearn/hamburger/
  2. 平均と偏差，分散，相関. http://www.takenet.or.jp/~hayakawa/u-tan1-1.htm
  3. t 分布. http://www.geisya.or.jp/~mwm48961/statistics/sample3.htm
  4. 池田 2013. 統計検定を理解せずに使っている人のために I. 化学と生物 51, 318-325.